Atom Mn: wielobit kwantowy. Jan Gaj Instytut Fizyki Doświadczalnej
|
|
|
- Roman Lewicki
- 5 lat temu
- Przeglądów:
Transkrypt
1 Atom Mn: wielobit kwantowy Jan Gaj Instytut Fizyki Doświadczalnej
2 Tomasz Kazimierczuk Mateusz Goryca Piotr Wojnar (IF PAN) Artur Trajnerowicz Andrzej Golnik Piotr Kossacki Jan Gaj Michał Nawrocki
3 Ostrzeżenia Będą uproszczenia. Wykrycie najbardziej skandalicznego może być nagrodzone. Decyzja należy do większości bez prawa veta wykładowcy. Będą pytania. Odpowiedź, która się najbardziej spodoba, może zostać nagrodzona. Decyzja należy do większości.
4 Motywacja: informatyka kwantowa Informatyka klasyczna: bit, przyjmuje dwie wartości: 0, 1 Informatyka kwantowa: qubit, występuje w stanach α 0 + β 1 ; α 2 + β 2 = 1 Komputera kwantowego dotychczas nie ma, ale jeśli powstanie, będzie rewolucja
5 Nagroda Fundacji na rzecz Nauki Polskiej 2008 Został uhonorowany wkład prof. Ryszarda Horodeckiego w stworzenie podstaw teoretycznych informatyki kwantowej, a w szczególności za wypracowanie podstaw praktycznej detekcji kwantowego splątania i odkrycie splątania związanego - "czarnych dziur w kwantowej teorii informacji.
6 Fundamentalna praca Science Citation Index 12/12/2008 Cited References Separability of mixed states: Necessary and sufficient conditions Horodecki M, Horodecki P, Horodecki R PHYSICS LETTERS A 223 (1-2): 1-8 NOV Document type: Article Language: English Cited References: 22 Times Cited: 849 Abstract: We provide necessary and sufficient conditions for the separability of mixed states. As a result we obtain a simple criterion of the separability for 2 x 2 and 2 x 3 systems. Here, the positivity of the partial transposition of a state is necessary and sufficient for its separability. However, this is not the case in general. Some examples of mixtures which demonstrate the utility of the criterion are considered.
7 Plan O qubicie O kropce kwantowej i ekscytonach Atom manganu w kropce Wykrywanie stanu (spinowego) manganu Jak sterować spinem manganu?
8 Jak zbudować qubit? Układ kwantowy o dwóch stanach własnych Dobra pamięć Szybka manipulacja Przykład: spin elektronu w kropce kwantowej Jon Mn: sześć stanów
9 Co to jest kropka kwantowa? Więzienie dla elektronów (dziur)
10 Półprzewodnik 1 Półprzewodnik 2 Półprzewodnik 1 T. Kazimierczuk
11 cqd.eecs.northwestern.edu
12 Jak zrobić kropkę kwantową?
13 MBE Epitaksja z wiązki molekularnej
14 Aparatura MBE
15 Samorosnące kropki kwantowe CdTe/ZnTe Wyhodowane przez Piotra Wojnara (IF PAN)
16 Jak obejrzeć kropki kwantowe? AFM Atomic Force Microscopy HRTEM High Resolution Transmission Electron Microscopy 2 nm 20 nm S. Kret, P. Dłużewski (IPPT PAN) P. Wojnar (IF PAN)
17 Jak pobudzić kropkę kwantową do świecenia?
18 Laser argonowy Pump laser Laser Dye laser barwnikowy T=1.5K Monochromator Spektrometr + CCD camera P1 P2 rozdzielczość przestrzenna 0.5 μm pole magnetyczne do 6T Cryostat Kriostatwith microscope objective T. Kazimierczuk
19 Jak badać świecenie jednej kropki?
20 -PL Intensity (arb. units) Mikrofotoluminescencja kropek kwantowych Mikroskop (rozdzielczość <1µm) T = 1.7K P = 700nW single QD emission CX XX CX' X
21 4000 P L intensity trion ujemny Xbiekscyton XX trion dodatni X+ ekscyton X biekscyton ujemny XX detection energy (mev) 1930 T. Kazimierczuk et al., 2008
22 Jak rozpoznać stan spinowy ekscytonu w kropce? Po polaryzacji kołowej fotonu σ+ σ-
23 polarization destroyed conserved reversed Lost (singlet) Jak się to mierzy? T. Kazimierczuk et al., 2008
24 Cy można przekazać spin z kropki do kropki? σ+ σ+ σ- σ-
25 Jak zrobić kropkę z jednym atomem Mn? CdTe (2 ml) (Cd,Mn)Te (0.05% Mn) CdTe (2 ml) cap layer (100 nm) (Cd,Zn)Te (0.8μm) CdTe (4μm) substrate (GaAs) Number of Mn ions in a single dot: ~1 Piotr Wojnar
26 Jak rozpoznać czy w kropce jest atom Mn?
27 X photoluminescence (arb. u.) XX CX energy (ev) 1.92 M. Goryca et al., 2008
28 E = Jσ X S Mn X Mn 5/2 3/2 σ+ 1/2-1/2-3/2-5/2 6 równoodległych stanów Energia przejścia spin manganu L. Besombes et al., PRL 93, (2004).
29 Jak rozpoznać stan spinowy atomu manganu w kropce? Dzięki oddziaływaniu ekscyton - mangan
30 Mn 5/2 3/2 σ+ 1/2-1/2-3/2-5/2 photoluminescence (arb. u.) X energy (ev) 6 równoodległych stanów Energia przejścia spin manganu M. Goryca et al., 2008
31 Odczytać widmo świecenia ekscytonu exc σ + exc linear 500 0T exc σ 500 X Mn 5/2 3/2 250 σ /2-1/2-3/ / E = Jσ X S Mn /2 3/2 σ /2-1/2-3/ E (ev) / M. Goryca et al., 2008
32 Jak wpływać na stan spinowy atomu manganu w kropce?
33 Natężenie luminescencji Mn E T. Kazimierczuk
34 Natężenie luminescencji Mn E T. Kazimierczuk
35 photoluminescence (arb. u.) B=+4.5T B=-4.5T Metoda działa, ale... wymaga sporego pola magnetycznego zmiana pola jest bardzo wolna energy (ev) M. Goryca et al., 2008
36 Jak inaczej wpływać na stan spinowy atomu manganu w kropce? Światłem (spolaryzowanym)
37 Światło kreuje nośniki o zadanym spinie Atom manganu jest Mn w otoczeniu spinowo spolaryzowanym Może się dostosuje? T. Kazimierczuk et al., arxiv: v1
38 Energia pobudzania (mev) Pobudzanie rezonansowe 2157 XX CX X Energia emisji (mev) M. Goryca et al., arxiv: v1
39 X Mn Jak szybko potrafimy zmieniać stan Mn? Pobudzanie σ+ Pobudzanie π B=1T Pobudzanie σ Energia emisji (mev) M. Goryca et al., 2008
40 Pamięć: setki µs I pobudzanie σ+ σ- σ+ T=1.5K, B=1T 42.9ns 1.0 PL intensity (arb.u.) t Manipulacja: dziesiątki ns ns 367ns 15.8ns exc 30µ w exc 10µ w exc 2.2µ w time (ns) 3000 M. Goryca et al., arxiv: v1
41 Emisja światła zdradza obecność ekscytonu w kropce kwantowej Polaryzacja światła świadczy o spinie ekscytonu Wykrywamy kropki z jednym atomem Mn Ustawiamy światłem spin atomu manganu Atom długo pamięta swój stan spinowy
42 Dziękuję za uwagę Nanoworld 2009, Kraków 9-11 stycznia
Ekscyton w morzu dziur
 Ekscyton w morzu dziur P. Kossacki, P. Płochocka, W. Maślana, A. Golnik, C. Radzewicz and J.A. Gaj Institute of Experimental Physics, Warsaw University S. Tatarenko, J. Cibert Laboratoire de Spectrométrie
Ekscyton w morzu dziur P. Kossacki, P. Płochocka, W. Maślana, A. Golnik, C. Radzewicz and J.A. Gaj Institute of Experimental Physics, Warsaw University S. Tatarenko, J. Cibert Laboratoire de Spectrométrie
Plan. Kropki kwantowe - część III spektroskopia pojedynczych kropek kwantowych. Kropki samorosnące. Kropki fluktuacje szerokości
 Plan Kropki kwantowe - część III spektroskopia pojedynczych kropek kwantowych Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika 1. Techniki pomiarowe 2. Podstawowe wyniki 3. Struktura
Plan Kropki kwantowe - część III spektroskopia pojedynczych kropek kwantowych Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika 1. Techniki pomiarowe 2. Podstawowe wyniki 3. Struktura
Kropki samorosnące. Optyka nanostruktur. Gęstość stanów. Kropki fluktuacje szerokości. Sebastian Maćkowski. InAs/GaAs QDs. Si/Ge QDs.
 Kropki samorosnące Optyka nanostruktur InAs/GaAs QDs Si/Ge QDs Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon:
Kropki samorosnące Optyka nanostruktur InAs/GaAs QDs Si/Ge QDs Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon:
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 2 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2013/14
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 2 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2013/14
Co to jest kropka kwantowa? Kropki kwantowe - część I otrzymywanie. Co to jest ekscyton? Co to jest ekscyton? e πε. E = n. Sebastian Maćkowski
 Co to jest kropka kwantowa? Kropki kwantowe - część I otrzymywanie Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Co to jest ekscyton? Co to jest ekscyton? h 2 2 2 e πε m* 4 0ε s Φ
Co to jest kropka kwantowa? Kropki kwantowe - część I otrzymywanie Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Co to jest ekscyton? Co to jest ekscyton? h 2 2 2 e πε m* 4 0ε s Φ
Mody sprzężone plazmon-fonon w silnych polach magnetycznych
 Mody sprzężone plazmon-fonon w silnych polach magnetycznych Mody sprzężone w półprzewodnikach polarnych + E E pl η = st α = E E pl ξ = p B.B. Varga,, Phys. Rev. 137,, A1896 (1965) A. Mooradian and B. Wright,
Mody sprzężone plazmon-fonon w silnych polach magnetycznych Mody sprzężone w półprzewodnikach polarnych + E E pl η = st α = E E pl ξ = p B.B. Varga,, Phys. Rev. 137,, A1896 (1965) A. Mooradian and B. Wright,
Współczesna fizyka ciała stałego
 Współczesna fizyka ciała stałego Struktury półprzewodnikowe o obniŝonej wymiarowości studnie kwantowe, druty kwantowe, kropki kwantowe fulereny, nanorurki, grafen Kwantowe efekty rozmiarowe Ograniczenie
Współczesna fizyka ciała stałego Struktury półprzewodnikowe o obniŝonej wymiarowości studnie kwantowe, druty kwantowe, kropki kwantowe fulereny, nanorurki, grafen Kwantowe efekty rozmiarowe Ograniczenie
Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych
 Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych Mody sprzęŝone w półprzewodnikach polarnych + E E pl η = st α = E E pl ξ = p B.B. Varga, Phys. Rev. 137,, A1896 (1965) A. Mooradian and B. Wright,
Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych Mody sprzęŝone w półprzewodnikach polarnych + E E pl η = st α = E E pl ξ = p B.B. Varga, Phys. Rev. 137,, A1896 (1965) A. Mooradian and B. Wright,
Pomiary widm fotoluminescencji
 Fotoluminescencja (PL photoluminescence) jako technika eksperymentalna, oznacza badanie zależności spektralnej rekombinacji promienistej, pochodzącej od nośników wzbudzonych optycznie. Schemat układu do
Fotoluminescencja (PL photoluminescence) jako technika eksperymentalna, oznacza badanie zależności spektralnej rekombinacji promienistej, pochodzącej od nośników wzbudzonych optycznie. Schemat układu do
Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych
 Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych Klasyczny przykład pośredniego oddziaływania pola magnetycznego na wzbudzenia fononowe Schemat: pole magnetyczne (siła Lorentza) nośniki (oddziaływanie
Mody sprzęŝone plazmon-fonon w silnych polach magnetycznych Klasyczny przykład pośredniego oddziaływania pola magnetycznego na wzbudzenia fononowe Schemat: pole magnetyczne (siła Lorentza) nośniki (oddziaływanie
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 2 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 2 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2014/15
Repeta z wykładu nr 11. Detekcja światła. Fluorescencja. Eksperyment optyczny. Sebastian Maćkowski
 Repeta z wykładu nr 11 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 CCD (urządzenie
Repeta z wykładu nr 11 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 CCD (urządzenie
Studnia kwantowa. Optyka nanostruktur. Studnia kwantowa. Gęstość stanów. Sebastian Maćkowski
 Studnia kwantowa Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Studnia kwantowa
Studnia kwantowa Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Studnia kwantowa
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 2 wykład: Piotr Fita pokazy: Jacek Szczytko ćwiczenia: Aneta Drabińska, Paweł Kowalczyk, Barbara Piętka Wydział Fizyki Uniwersytet
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 2 wykład: Piotr Fita pokazy: Jacek Szczytko ćwiczenia: Aneta Drabińska, Paweł Kowalczyk, Barbara Piętka Wydział Fizyki Uniwersytet
Wzrost pseudomorficzny. Optyka nanostruktur. Mody wzrostu. Ekscyton. Sebastian Maćkowski
 Wzrost pseudomorficzny Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 naprężenie
Wzrost pseudomorficzny Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 naprężenie
Podstawy informatyki kwantowej
 Wykład 6 27 kwietnia 2016 Podstawy informatyki kwantowej dr hab. Łukasz Cywiński lcyw@ifpan.edu.pl http://info.ifpan.edu.pl/~lcyw/ Wykłady: 6, 13, 20, 27 kwietnia oraz 4 maja (na ostatnim wykładzie będzie
Wykład 6 27 kwietnia 2016 Podstawy informatyki kwantowej dr hab. Łukasz Cywiński lcyw@ifpan.edu.pl http://info.ifpan.edu.pl/~lcyw/ Wykłady: 6, 13, 20, 27 kwietnia oraz 4 maja (na ostatnim wykładzie będzie
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 2 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2015/16
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 2 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Anna Grochola, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2015/16
Informatyka kwantowa i jej fizyczne podstawy Rezonans spinowy, bramki dwu-kubitowe
 Wykład 4 29 kwietnia 2015 Informatyka kwantowa i jej fizyczne podstawy Rezonans spinowy, bramki dwu-kubitowe Łukasz Cywiński lcyw@ifpan.edu.pl http://info.ifpan.edu.pl/~lcyw/ Dobra lektura: Michel Le Bellac
Wykład 4 29 kwietnia 2015 Informatyka kwantowa i jej fizyczne podstawy Rezonans spinowy, bramki dwu-kubitowe Łukasz Cywiński lcyw@ifpan.edu.pl http://info.ifpan.edu.pl/~lcyw/ Dobra lektura: Michel Le Bellac
Nierównowagowe kondensaty polarytonów ekscytonowych z gigantycznym rozszczepieniem Zeemana w mikrownękach półprzewodnikowych
 Nierównowagowe kondensaty polarytonów ekscytonowych z gigantycznym rozszczepieniem Zeemana w mikrownękach półprzewodnikowych B. Piętka, M. Król, R. Mirek, K. Lekenta, J. Szczytko J.-G. Rousset, M. Nawrocki,
Nierównowagowe kondensaty polarytonów ekscytonowych z gigantycznym rozszczepieniem Zeemana w mikrownękach półprzewodnikowych B. Piętka, M. Król, R. Mirek, K. Lekenta, J. Szczytko J.-G. Rousset, M. Nawrocki,
Współczesna fizyka ciała stałego
 Współczesna fizyka ciała stałego Struktury półprzewodnikowe o obniżonej wymiarowości studnie kwantowe, druty kwantowe, kropki kwantowe.. fulereny, nanorurki, grafen. Kwantowe efekty rozmiarowe Ograniczenie
Współczesna fizyka ciała stałego Struktury półprzewodnikowe o obniżonej wymiarowości studnie kwantowe, druty kwantowe, kropki kwantowe.. fulereny, nanorurki, grafen. Kwantowe efekty rozmiarowe Ograniczenie
Domieszki w półprzewodnikach
 Domieszki w półprzewodnikach Niebieska optoelektronika Niebieski laser Nie można obecnie wyświetlić tego obrazu. Domieszkowanie m* O Neutralny donor w przybliżeniu masy efektywnej 2 2 0 2 * 2 * 13.6 *
Domieszki w półprzewodnikach Niebieska optoelektronika Niebieski laser Nie można obecnie wyświetlić tego obrazu. Domieszkowanie m* O Neutralny donor w przybliżeniu masy efektywnej 2 2 0 2 * 2 * 13.6 *
UNIWERSYTET SZCZECIŃSKI INSTYTUT FIZYKI ZAKŁAD FIZYKI CIAŁA STAŁEGO. Ćwiczenie laboratoryjne Nr.2. Elektroluminescencja
 UNIWERSYTET SZCZECIŃSKI INSTYTUT FIZYKI ZAKŁAD FIZYKI CIAŁA STAŁEGO Ćwiczenie laboratoryjne Nr.2 Elektroluminescencja SZCZECIN 2002 WSTĘP Mianem elektroluminescencji określamy zjawisko emisji spontanicznej
UNIWERSYTET SZCZECIŃSKI INSTYTUT FIZYKI ZAKŁAD FIZYKI CIAŁA STAŁEGO Ćwiczenie laboratoryjne Nr.2 Elektroluminescencja SZCZECIN 2002 WSTĘP Mianem elektroluminescencji określamy zjawisko emisji spontanicznej
Domieszki w półprzewodnikach
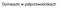 Domieszki w półprzewodnikach Niebieska optoelektronika Niebieski laser Elektryczne pobudzanie struktury laserowej Unipress 106 unipress 8 Moc op ptyczna ( mw ) 6 4 2 0 0.0 0.5 1.0 1.5 2.0 Natężenie prądu
Domieszki w półprzewodnikach Niebieska optoelektronika Niebieski laser Elektryczne pobudzanie struktury laserowej Unipress 106 unipress 8 Moc op ptyczna ( mw ) 6 4 2 0 0.0 0.5 1.0 1.5 2.0 Natężenie prądu
półprzewodniki Plan na dzisiaj Optyka nanostruktur Struktura krystaliczna Dygresja Sebastian Maćkowski
 Plan na dzisiaj Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 półprzewodniki
Plan na dzisiaj Optyka nanostruktur Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 półprzewodniki
W5. Komputer kwantowy
 W5. Komputer kwantowy Komputer klasyczny: Informacja zapisana w postaci bitów (binary digit) (sygnał jest albo go nie ma) W klasycznych komputerach wartość bitu jest określona przez stan pewnego elementu
W5. Komputer kwantowy Komputer klasyczny: Informacja zapisana w postaci bitów (binary digit) (sygnał jest albo go nie ma) W klasycznych komputerach wartość bitu jest określona przez stan pewnego elementu
Wysokowydajne falowodowe źródło skorelowanych par fotonów
 Wysokowydajne falowodowe źródło skorelowanych par fotonów Michał Karpioski * Konrad Banaszek, Czesław Radzewicz * * Instytut Fizyki Doświadczalnej, Instytut Fizyki Teoretycznej Wydział Fizyki Uniwersytet
Wysokowydajne falowodowe źródło skorelowanych par fotonów Michał Karpioski * Konrad Banaszek, Czesław Radzewicz * * Instytut Fizyki Doświadczalnej, Instytut Fizyki Teoretycznej Wydział Fizyki Uniwersytet
Idea przyłączenie chromoforu (fluoryzującego) do biomolekuły
 markery, nanocząstki, kropki kwantowe Idea przyłączenie chromoforu (fluoryzującego) do biomolekuły sondy fluorescencyjnej wizualizacja przez oświetlenie odpow. światłem obrazowanie (możliwe poniżej dyfrakcyjnego
markery, nanocząstki, kropki kwantowe Idea przyłączenie chromoforu (fluoryzującego) do biomolekuły sondy fluorescencyjnej wizualizacja przez oświetlenie odpow. światłem obrazowanie (możliwe poniżej dyfrakcyjnego
Operacje na spinie pojedynczego elektronu w zastosowaniu do budowy bramek logicznych komputera kwantowego
 Stanisław Bednarek Zespół Teorii Nanostruktur i Nanourządzeń Katedra Informatyki Stosowanej i Fizyki Komputerowej WFiIS AGH Operacje na spinie pojedynczego elektronu w zastosowaniu do budowy bramek logicznych
Stanisław Bednarek Zespół Teorii Nanostruktur i Nanourządzeń Katedra Informatyki Stosowanej i Fizyki Komputerowej WFiIS AGH Operacje na spinie pojedynczego elektronu w zastosowaniu do budowy bramek logicznych
Wykład 12 V = 4 km/s E 0 =.08 e V e = = 1 Å
 Wykład 12 Fale materii: elektrony, neutrony, lekkie atomy Neutrony generowane w reaktorze są spowalniane w wyniku zderzeń z moderatorem (grafitem) do V = 4 km/s, co odpowiada energii E=0.08 ev a energia
Wykład 12 Fale materii: elektrony, neutrony, lekkie atomy Neutrony generowane w reaktorze są spowalniane w wyniku zderzeń z moderatorem (grafitem) do V = 4 km/s, co odpowiada energii E=0.08 ev a energia
W stronę plazmonowego wzmocnienia efektów magnetooptycznych
 W stronę plazmonowego wzmocnienia efektów magnetooptycznych Joanna Papierska J. Suffczyński, M. Koperski, P. Nowicki, B. Witkowski, M. Godlewski, A. Navarro-Quezada, A. Bonanni Warsztaty NanoWorld 2011,
W stronę plazmonowego wzmocnienia efektów magnetooptycznych Joanna Papierska J. Suffczyński, M. Koperski, P. Nowicki, B. Witkowski, M. Godlewski, A. Navarro-Quezada, A. Bonanni Warsztaty NanoWorld 2011,
Jak TO działa? Co to są półprzewodniki? TRENDY: Prawo Moore a. Google: Jacek Szczytko Login: student Hasło: *******
 Co to są półprzewodniki? Jak TO działa? http://www.fuw.edu.pl/~szczytko/ Google: Jacek Szczytko Login: student Hasło: ******* Jacek.Szczytko@fuw.edu.pl Wydział Fizyki UW 2 TRENDY: Prawo Moore a TRENDY:
Co to są półprzewodniki? Jak TO działa? http://www.fuw.edu.pl/~szczytko/ Google: Jacek Szczytko Login: student Hasło: ******* Jacek.Szczytko@fuw.edu.pl Wydział Fizyki UW 2 TRENDY: Prawo Moore a TRENDY:
Autoreferat. 1. Imię i Nazwisko Posiadane dyplomy, stopnie naukowe... 2
 Piotr Wojnar Instytut Fizyki, Polskiej Akademii Nauk Warszawa, 2016 Autoreferat Spis treści: 1. Imię i Nazwisko... 2 2. Posiadane dyplomy, stopnie naukowe... 2 3. Informacja o dotychczasowym zatrudnieniu
Piotr Wojnar Instytut Fizyki, Polskiej Akademii Nauk Warszawa, 2016 Autoreferat Spis treści: 1. Imię i Nazwisko... 2 2. Posiadane dyplomy, stopnie naukowe... 2 3. Informacja o dotychczasowym zatrudnieniu
II.6 Atomy w zewnętrznym polu magnetycznym
 II.6 Atomy w zewnętrznym polu magnetycznym 1. Kwantowanie przestrzenne w zewnętrznym polu magnetycznym. Model wektorowy raz jeszcze 2. Zjawisko Zeemana Normalne zjawisko Zeemana i jego wyjaśnienie w modelu
II.6 Atomy w zewnętrznym polu magnetycznym 1. Kwantowanie przestrzenne w zewnętrznym polu magnetycznym. Model wektorowy raz jeszcze 2. Zjawisko Zeemana Normalne zjawisko Zeemana i jego wyjaśnienie w modelu
Fluorescencyjna detekcja śladów cząstek jądrowych przy użyciu kryształów fluorku litu
 Fluorescencyjna detekcja śladów cząstek jądrowych przy użyciu kryształów fluorku litu Paweł Bilski Zakład Fizyki Radiacyjnej i Dozymetrii (NZ63) IFJ PAN Fluorescenscent Nuclear Track Detectors (FNTD) pierwsza
Fluorescencyjna detekcja śladów cząstek jądrowych przy użyciu kryształów fluorku litu Paweł Bilski Zakład Fizyki Radiacyjnej i Dozymetrii (NZ63) IFJ PAN Fluorescenscent Nuclear Track Detectors (FNTD) pierwsza
Podstawy fizyki wykład 2
 D. Halliday, R. Resnick, J.Walker: Podstawy Fizyki, tom 5, PWN, Warszawa 2003. H. D. Young, R. A. Freedman, Sear s & Zemansky s University Physics with Modern Physics, Addison-Wesley Publishing Company,
D. Halliday, R. Resnick, J.Walker: Podstawy Fizyki, tom 5, PWN, Warszawa 2003. H. D. Young, R. A. Freedman, Sear s & Zemansky s University Physics with Modern Physics, Addison-Wesley Publishing Company,
POLITECHNIKA GDAŃSKA WYDZIAŁ FIZYKI TECHNICZNEJ I MATEMATYKI STOSOWANEJ EKSCYTONY. Seminarium z Molekularnego Ciała a Stałego Jędrzejowski Jaromir
 POLITECHNIKA GDAŃSKA WYDZIAŁ FIZYKI TECHNICZNEJ I MATEMATYKI STOSOWANEJ EKSCYTONY W CIAŁACH ACH STAŁYCH Seminarium z Molekularnego Ciała a Stałego Jędrzejowski Jaromir Co to sąs ekscytony? ekscyton to
POLITECHNIKA GDAŃSKA WYDZIAŁ FIZYKI TECHNICZNEJ I MATEMATYKI STOSOWANEJ EKSCYTONY W CIAŁACH ACH STAŁYCH Seminarium z Molekularnego Ciała a Stałego Jędrzejowski Jaromir Co to sąs ekscytony? ekscyton to
Własności optyczne półprzewodników
 Własności optyczne półprzewodników Andrzej Wysmołek Wykład przygotowany w oparciu o wykłady prowadzone na Wydziale Fizyki UW przez prof. Mariana Grynberga oraz prof. Romana Stępniewskiego Klasyfikacja
Własności optyczne półprzewodników Andrzej Wysmołek Wykład przygotowany w oparciu o wykłady prowadzone na Wydziale Fizyki UW przez prof. Mariana Grynberga oraz prof. Romana Stępniewskiego Klasyfikacja
Teoria Orbitali Molekularnych. tworzenie wiązań chemicznych
 Teoria Orbitali Molekularnych tworzenie wiązań chemicznych Zbliżanie się atomów aż do momentu nałożenia się ich orbitali H a +H b H a H b Wykres obrazujący zależność energii od odległości atomów długość
Teoria Orbitali Molekularnych tworzenie wiązań chemicznych Zbliżanie się atomów aż do momentu nałożenia się ich orbitali H a +H b H a H b Wykres obrazujący zależność energii od odległości atomów długość
Uniwersytet Warszawski Wydział Fizyki. Badanie efektu Faraday a w kryształach CdTe i CdMnTe
 Uniwersytet Warszawski Wydział Fizyki Marcin Polkowski 251328 Badanie efektu Faraday a w kryształach CdTe i CdMnTe Pracownia Fizyczna dla Zaawansowanych ćwiczenie F8 w zakresie Fizyki Ciała Stałego Streszczenie
Uniwersytet Warszawski Wydział Fizyki Marcin Polkowski 251328 Badanie efektu Faraday a w kryształach CdTe i CdMnTe Pracownia Fizyczna dla Zaawansowanych ćwiczenie F8 w zakresie Fizyki Ciała Stałego Streszczenie
Świat klasyczny i kwantowy por. WYKŁAD nr 2. Splątane stany - EPR. por. WYKŁAD nr 2. Kwantowa kryptografia i teleportacja. Splątanie kwantowe
 Kwantowa kryptografia i teleportacja. Splątanie kwantowe Świat klasyczny i kwantowy por. WYKŁAD nr a. Poplątane stany. i. Eksperyment EPR. ii. Eksperyment Bella b. Star-Trec, czyli teleportujcie mnie!
Kwantowa kryptografia i teleportacja. Splątanie kwantowe Świat klasyczny i kwantowy por. WYKŁAD nr a. Poplątane stany. i. Eksperyment EPR. ii. Eksperyment Bella b. Star-Trec, czyli teleportujcie mnie!
Nanofizyka co wiemy, a czego jeszcze szukamy?
 Nanofizyka co wiemy, a czego jeszcze szukamy? Maciej Maśka Zakład Fizyki Teoretycznej UŚ Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego ...czyli dlaczego NANO
Nanofizyka co wiemy, a czego jeszcze szukamy? Maciej Maśka Zakład Fizyki Teoretycznej UŚ Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego ...czyli dlaczego NANO
II.4 Kwantowy moment pędu i kwantowy moment magnetyczny w modelu wektorowym
 II.4 Kwantowy moment pędu i kwantowy moment magnetyczny w modelu wektorowym Jan Królikowski Fizyka IVBC 1 II.4.1 Ogólne własności wektora kwantowego momentu pędu Podane poniżej własności kwantowych wektorów
II.4 Kwantowy moment pędu i kwantowy moment magnetyczny w modelu wektorowym Jan Królikowski Fizyka IVBC 1 II.4.1 Ogólne własności wektora kwantowego momentu pędu Podane poniżej własności kwantowych wektorów
WYBRANE TECHNIKI SPEKTROSKOPII LASEROWEJ ROZDZIELCZEJ W CZASIE prof. Halina Abramczyk Laboratory of Laser Molecular Spectroscopy
 WYBRANE TECHNIKI SPEKTROSKOPII LASEROWEJ ROZDZIELCZEJ W CZASIE 1 Ze względu na rozdzielczość czasową metody, zależną od długości trwania impulsu, spektroskopię dzielimy na: nanosekundową (10-9 s) pikosekundową
WYBRANE TECHNIKI SPEKTROSKOPII LASEROWEJ ROZDZIELCZEJ W CZASIE 1 Ze względu na rozdzielczość czasową metody, zależną od długości trwania impulsu, spektroskopię dzielimy na: nanosekundową (10-9 s) pikosekundową
Wstęp do Optyki i Fizyki Materii Skondensowanej
 Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 1 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Paweł Kowalczyk, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2015/16
Wstęp do Optyki i Fizyki Materii Skondensowanej Część I: Optyka, wykład 1 wykład: Piotr Fita pokazy: Andrzej Wysmołek ćwiczenia: Paweł Kowalczyk, Barbara Piętka Wydział Fizyki Uniwersytet Warszawski 2015/16
fotony i splątanie Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW
 fotony i splątanie Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW wektory pojedyncze fotony paradoks EPR Wielkości wektorowe w fizyce punkt zaczepienia
fotony i splątanie Jacek Matulewski Karolina Słowik Jarosław Zaremba Jacek Jurkowski MECHANIKA KWANTOWA DLA NIEFIZYKÓW wektory pojedyncze fotony paradoks EPR Wielkości wektorowe w fizyce punkt zaczepienia
Podstawy fizyki ciała stałego półprzewodniki domieszkowane
 Podstawy fizyki ciała stałego półprzewodniki domieszkowane Półprzewodnik typu n IV-Ge V-As Jeżeli pięciowartościowy atom V-As zastąpi w sieci atom IV-Ge to cztery elektrony biorą udział w wiązaniu kowalentnym,
Podstawy fizyki ciała stałego półprzewodniki domieszkowane Półprzewodnik typu n IV-Ge V-As Jeżeli pięciowartościowy atom V-As zastąpi w sieci atom IV-Ge to cztery elektrony biorą udział w wiązaniu kowalentnym,
Widmo promieniowania elektromagnetycznego Czułość oka człowieka
 dealna charakterystyka prądowonapięciowa złącza p-n ev ( V ) = 0 exp 1 kbt Przebicie złącza przy polaryzacji zaporowej Przebicie Zenera tunelowanie elektronów przez wąską warstwę zaporową w złączu silnie
dealna charakterystyka prądowonapięciowa złącza p-n ev ( V ) = 0 exp 1 kbt Przebicie złącza przy polaryzacji zaporowej Przebicie Zenera tunelowanie elektronów przez wąską warstwę zaporową w złączu silnie
 2013 02 27 2 1. Jakie warstwy zostały wyhodowane w celu uzyskania 2DEG? (szkic?) 2. Gdzie było domieszkowanie? Dlaczego jako domieszek użyto w próbce atomy krzemu? 3. Jaki kształt miała próbka? 4. W jaki
2013 02 27 2 1. Jakie warstwy zostały wyhodowane w celu uzyskania 2DEG? (szkic?) 2. Gdzie było domieszkowanie? Dlaczego jako domieszek użyto w próbce atomy krzemu? 3. Jaki kształt miała próbka? 4. W jaki
Własności optyczne półprzewodników
 Własności optyczne półprzewodników Andrzej Wysmołek Wykład przygotowany w oparciu o wykłady prowadzone na Wydziale Fizyki Uniwersytetu Warszawakiego przez prof. Mariana Grynberga oraz prof. Romana Stępniewskiego
Własności optyczne półprzewodników Andrzej Wysmołek Wykład przygotowany w oparciu o wykłady prowadzone na Wydziale Fizyki Uniwersytetu Warszawakiego przez prof. Mariana Grynberga oraz prof. Romana Stępniewskiego
Nanostruktury, spintronika, komputer kwantowy
 Nanostruktury, spintronika, komputer kwantowy Wykªad dla uczniów Gimnazjum Nr 2 w Krakowie I. Nanostruktury Skala mikrometrowa 1µm (mikrometr) = 1 milionowa cz ± metra = 10 6 m obiekty mikrometrowe, np.
Nanostruktury, spintronika, komputer kwantowy Wykªad dla uczniów Gimnazjum Nr 2 w Krakowie I. Nanostruktury Skala mikrometrowa 1µm (mikrometr) = 1 milionowa cz ± metra = 10 6 m obiekty mikrometrowe, np.
Atom wodoru. Model klasyczny: nieruchome jądro +p i poruszający się wokół niego elektron e w odległości r; energia potencjalna elektronu:
 ATOM WODORU Atom wodoru Model klasyczny: nieruchome jądro +p i poruszający się wokół niego elektron e w odległości r; energia potencjalna elektronu: U = 4πε Opis kwantowy: wykorzystując zasadę odpowiedniości
ATOM WODORU Atom wodoru Model klasyczny: nieruchome jądro +p i poruszający się wokół niego elektron e w odległości r; energia potencjalna elektronu: U = 4πε Opis kwantowy: wykorzystując zasadę odpowiedniości
- wiązki pompująca & próbkująca oddziaływanie selektywne prędkościowo widma bezdopplerowskie T. 0 k. z L 0 k. L 0 k
 Podsumowanie W1 Lasery w spektroskopii atomowej/molekularnej a) spektroskopia klasyczna b) spektroskopia bezdopplerowska 1. Spektroskopia nasyceniowa - wiązki pompująca & próbkująca oddziaływanie selektywne
Podsumowanie W1 Lasery w spektroskopii atomowej/molekularnej a) spektroskopia klasyczna b) spektroskopia bezdopplerowska 1. Spektroskopia nasyceniowa - wiązki pompująca & próbkująca oddziaływanie selektywne
Henryk Szymczak Instytut Fizyki PAN
 NNnnNowe kwazicząstki w magnetykach Henryk Szymczak Instytut Fizyki PAN Zjazd Fizyków 2015 1 Enrico Fermi: nigdy nie należy lekceważyć przyjemności, jaką każdy z nas odczuwa, słysząc coś, o czym już wie
NNnnNowe kwazicząstki w magnetykach Henryk Szymczak Instytut Fizyki PAN Zjazd Fizyków 2015 1 Enrico Fermi: nigdy nie należy lekceważyć przyjemności, jaką każdy z nas odczuwa, słysząc coś, o czym już wie
SPM Scanning Probe Microscopy Mikroskopia skanującej sondy STM Scanning Tunneling Microscopy Skaningowa mikroskopia tunelowa AFM Atomic Force
 SPM Scanning Probe Microscopy Mikroskopia skanującej sondy STM Scanning Tunneling Microscopy Skaningowa mikroskopia tunelowa AFM Atomic Force Microscopy Mikroskopia siły atomowej MFM Magnetic Force Microscopy
SPM Scanning Probe Microscopy Mikroskopia skanującej sondy STM Scanning Tunneling Microscopy Skaningowa mikroskopia tunelowa AFM Atomic Force Microscopy Mikroskopia siły atomowej MFM Magnetic Force Microscopy
Pytać! Nanotechnologie (II) Jeszcze o teoriach (nie tylko fizycznych)
 Nanotechnologie (II) Jeszcze o teoriach (nie tylko fizycznych) Rys. źródło: Internet Jacek.Szczytko@fuw.edu.pl http://www.fuw.edu.pl/~szczytko Półprzewodniki a.studnie i.studnie i ekscytony ii.lasery iii.dwuwymiarowe
Nanotechnologie (II) Jeszcze o teoriach (nie tylko fizycznych) Rys. źródło: Internet Jacek.Szczytko@fuw.edu.pl http://www.fuw.edu.pl/~szczytko Półprzewodniki a.studnie i.studnie i ekscytony ii.lasery iii.dwuwymiarowe
WYZNACZANIE STAŁEJ PLANCKA Z POMIARU CHARAKTERYSTYK PRĄDOWO-NAPIĘCIOWYCH DIOD ELEKTROLUMINESCENCYJNYCH. Irena Jankowska-Sumara, Magdalena Krupska
 1 II PRACOWNIA FIZYCZNA: FIZYKA ATOMOWA Z POMIARU CHARAKTERYSTYK PRĄDOWO-NAPIĘCIOWYCH DIOD ELEKTROLUMINESCENCYJNYCH Irena Jankowska-Sumara, Magdalena Krupska Cel ćwiczenia Celem ćwiczenia jest wyznaczenie
1 II PRACOWNIA FIZYCZNA: FIZYKA ATOMOWA Z POMIARU CHARAKTERYSTYK PRĄDOWO-NAPIĘCIOWYCH DIOD ELEKTROLUMINESCENCYJNYCH Irena Jankowska-Sumara, Magdalena Krupska Cel ćwiczenia Celem ćwiczenia jest wyznaczenie
Korelacje przestrzenne między nośnikami uwięzionymi w półprzewodnikowych kropkach kwantowych. Bartłomiej Szafran
 Korelacje przestrzenne między nośnikami uwięzionymi w półprzewodnikowych kropkach kwantowych (wybrane wyniki z rozprawy habilitacyjnej) Kraków 12.05.2006 Bartłomiej Szafran Półprzewodnikowe kropki kwantowe
Korelacje przestrzenne między nośnikami uwięzionymi w półprzewodnikowych kropkach kwantowych (wybrane wyniki z rozprawy habilitacyjnej) Kraków 12.05.2006 Bartłomiej Szafran Półprzewodnikowe kropki kwantowe
I. PROMIENIOWANIE CIEPLNE
 I. PROMIENIOWANIE CIEPLNE - lata '90 XIX wieku WSTĘP Widmo promieniowania elektromagnetycznego zakres "pokrycia" różnymi rodzajami fal elektromagnetycznych promieniowania zawartego w danej wiązce. rys.i.1.
I. PROMIENIOWANIE CIEPLNE - lata '90 XIX wieku WSTĘP Widmo promieniowania elektromagnetycznego zakres "pokrycia" różnymi rodzajami fal elektromagnetycznych promieniowania zawartego w danej wiązce. rys.i.1.
Wykład IV. Półprzewodniki samoistne i domieszkowe
 Wykład IV Półprzewodniki samoistne i domieszkowe Półprzewodniki (Si, Ge, GaAs) Konfiguracja elektronowa Si : 1s 2 2s 2 2p 6 3s 2 3p 2 = [Ne] 3s 2 3p 2 4 elektrony walencyjne Półprzewodnik samoistny Talent
Wykład IV Półprzewodniki samoistne i domieszkowe Półprzewodniki (Si, Ge, GaAs) Konfiguracja elektronowa Si : 1s 2 2s 2 2p 6 3s 2 3p 2 = [Ne] 3s 2 3p 2 4 elektrony walencyjne Półprzewodnik samoistny Talent
Wytwarzanie niskowymiarowych struktur półprzewodnikowych
 Większość struktur niskowymiarowych wytwarzanych jest za pomocą technik epitaksjalnych. Najczęściej wykorzystywane metody wzrostu: - epitaksja z wiązki molekularnej (MBE Molecular Beam Epitaxy) - epitaksja
Większość struktur niskowymiarowych wytwarzanych jest za pomocą technik epitaksjalnych. Najczęściej wykorzystywane metody wzrostu: - epitaksja z wiązki molekularnej (MBE Molecular Beam Epitaxy) - epitaksja
MIKROSKOPIA ELEKTRONOWA. Publikacja współfinansowana ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego
 MIKROSKOPIA ELEKTRONOWA Publikacja współfinansowana ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Tło historyczne Pod koniec XIX wieku stosowanie mikroskopów świetlnych w naukach
MIKROSKOPIA ELEKTRONOWA Publikacja współfinansowana ze środków Unii Europejskiej w ramach Europejskiego Funduszu Społecznego Tło historyczne Pod koniec XIX wieku stosowanie mikroskopów świetlnych w naukach
Repeta z wykładu nr 8. Detekcja światła. Przypomnienie. Efekt fotoelektryczny
 Repeta z wykładu nr 8 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 przegląd detektorów
Repeta z wykładu nr 8 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 przegląd detektorów
Spektroskopia Ramanowska
 Spektroskopia Ramanowska Część A 1.Krótki wstęp historyczny 2.Oddziaływanie światła z osrodkiem materialnym (rozpraszanie światła) 3.Opis klasyczny zjawiska Ramana 4. Widmo ramanowskie. 5. Opis półklasyczny
Spektroskopia Ramanowska Część A 1.Krótki wstęp historyczny 2.Oddziaływanie światła z osrodkiem materialnym (rozpraszanie światła) 3.Opis klasyczny zjawiska Ramana 4. Widmo ramanowskie. 5. Opis półklasyczny
Półprzewodnikowe kropki kwantowe
 Jest to zapis odczytu wygłoszonego na XXXIII Szkole Matematyki Poglądowej Metody klasyczne i współczesne, sierpień 2004. Rys. 1. Kolejne fazy wzrostu kryształu metodą Czochralskiego Półprzewodnikowe kropki
Jest to zapis odczytu wygłoszonego na XXXIII Szkole Matematyki Poglądowej Metody klasyczne i współczesne, sierpień 2004. Rys. 1. Kolejne fazy wzrostu kryształu metodą Czochralskiego Półprzewodnikowe kropki
Fizyka 2. Janusz Andrzejewski
 Fizyka 2 wykład 14 Janusz Andrzejewski Atom wodoru Wczesne modele atomu -W czasach Newtona atom uważany była za małą twardą kulkę co dość dobrze sprawdzało się w rozważaniach dotyczących kinetycznej teorii
Fizyka 2 wykład 14 Janusz Andrzejewski Atom wodoru Wczesne modele atomu -W czasach Newtona atom uważany była za małą twardą kulkę co dość dobrze sprawdzało się w rozważaniach dotyczących kinetycznej teorii
Początek XX wieku. Dualizm korpuskularno - falowy
 Początek XX wieku Światło: fala czy cząstka? Kwantowanie energii promieniowania termicznego postulat Plancka efekt fotoelektryczny efekt Comptona Fale materii de Broglie a Dualizm korpuskularno - falowy
Początek XX wieku Światło: fala czy cząstka? Kwantowanie energii promieniowania termicznego postulat Plancka efekt fotoelektryczny efekt Comptona Fale materii de Broglie a Dualizm korpuskularno - falowy
Świat klasyczny i kwantowy
 Kwantowa kryptografia i teleportacja. Splątanie kwantowe Prawo Moore a Jacek.Szczytko@fuw.edu.pl http://www.fuw.edu.pl/~szczytko/nt.4. Prace zaliczeniowe! Zadania Studenckie Do zaliczenia wykładu wymagana
Kwantowa kryptografia i teleportacja. Splątanie kwantowe Prawo Moore a Jacek.Szczytko@fuw.edu.pl http://www.fuw.edu.pl/~szczytko/nt.4. Prace zaliczeniowe! Zadania Studenckie Do zaliczenia wykładu wymagana
Wprowadzenie do ekscytonów
 Proces absorpcji można traktować jako tworzenie się, pod wpływem zewnętrznego pola elektrycznego, pary elektron-dziura, które mogą być opisane w przybliżeniu jednoelektronowym. Dokładniejszym podejściem
Proces absorpcji można traktować jako tworzenie się, pod wpływem zewnętrznego pola elektrycznego, pary elektron-dziura, które mogą być opisane w przybliżeniu jednoelektronowym. Dokładniejszym podejściem
INSTYTUT FIZYKI POLSKIEJ AKADEMII NAUK
 INSTYTUT FIZYKI POLSKIEJ AKADEMII NAUK INSTITUTE OF PHYSICS, POLISH ACADEMY OF SCIENCES 02-668 WARSZAWA, Al. LOTNIKÓW 32/46 fax: + (48-22) 843-0926; http://info.ifpan.edu.pl LABORATORY OF GROWTH AND PHYSICS
INSTYTUT FIZYKI POLSKIEJ AKADEMII NAUK INSTITUTE OF PHYSICS, POLISH ACADEMY OF SCIENCES 02-668 WARSZAWA, Al. LOTNIKÓW 32/46 fax: + (48-22) 843-0926; http://info.ifpan.edu.pl LABORATORY OF GROWTH AND PHYSICS
Repeta z wykładu nr 4. Detekcja światła. Dygresja. Plan na dzisiaj
 Repeta z wykładu nr 4 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Repeta z wykładu nr 4 Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje:
Prezentacja aparatury zakupionej przez IKiFP. Mikroskopy LEEM i PEEM
 Prezentacja aparatury zakupionej przez IKiFP Mikroskopy LEEM i PEEM Cechy ogólne mikroskopów do badania powierzchni; czułość Å - nm szeroka gama kontrastów topograficzny strukturalny chemiczny magnetyczny
Prezentacja aparatury zakupionej przez IKiFP Mikroskopy LEEM i PEEM Cechy ogólne mikroskopów do badania powierzchni; czułość Å - nm szeroka gama kontrastów topograficzny strukturalny chemiczny magnetyczny
Efektywne symulacje mikromagnetyczne układów magnonicznych przy wykorzystaniu GPGPU.
 Efektywne symulacje mikromagnetyczne układów magnonicznych przy wykorzystaniu GPGPU. Mateusz Zelent, Paweł Gruszecki, Michał Mruczkiewicz, Maciej Krawczyk Wydział Fizyki, Zakład Fizyki Nanomateriałów Fale
Efektywne symulacje mikromagnetyczne układów magnonicznych przy wykorzystaniu GPGPU. Mateusz Zelent, Paweł Gruszecki, Michał Mruczkiewicz, Maciej Krawczyk Wydział Fizyki, Zakład Fizyki Nanomateriałów Fale
Bity, P-bity, Q-bity. Quantum Computer II (QC) Bramki kubitowe. Bramki kubitowe HARDWARE. Jacek.Szczytko@fuw.edu.pl. Jacek.Szczytko@fuw.edu.
 Quantum Computer II (QC) Jacek Szczytko, Wydział Fizyki UW. a. Logika bramek b. Kwantowe algorytmy c. Jak zbudować taki komputer? HARDWARE Bity, P-bity, Q-bity Kwantowym odpowiednikiem klasycznego bitu
Quantum Computer II (QC) Jacek Szczytko, Wydział Fizyki UW. a. Logika bramek b. Kwantowe algorytmy c. Jak zbudować taki komputer? HARDWARE Bity, P-bity, Q-bity Kwantowym odpowiednikiem klasycznego bitu
InTechFun. Innowacyjne technologie wielofunkcyjnych materiałów i struktur dla nanoelektroniki, fotoniki, spintroniki i technik sensorowych
 Innowacyjne technologie wielofunkcyjnych materiałów i struktur dla nanoelektroniki, fotoniki, spintroniki i technik sensorowych InTechFun Instytut Fizyki Polskiej Akademii Nauk Zbigniew R. Żytkiewicz IF
Innowacyjne technologie wielofunkcyjnych materiałów i struktur dla nanoelektroniki, fotoniki, spintroniki i technik sensorowych InTechFun Instytut Fizyki Polskiej Akademii Nauk Zbigniew R. Żytkiewicz IF
Wady ostrza. Ponieważ ostrze ma duży promień niektóre elementy ukształtowania powierzchni nie są rejestrowane (fioletowy element)
 Wady ostrza Ponieważ ostrze ma duży promień niektóre elementy ukształtowania powierzchni nie są rejestrowane (fioletowy element) Ponieważ ostrze ma kilka zakończeń w obrazie pojawiają się powtórzone struktury
Wady ostrza Ponieważ ostrze ma duży promień niektóre elementy ukształtowania powierzchni nie są rejestrowane (fioletowy element) Ponieważ ostrze ma kilka zakończeń w obrazie pojawiają się powtórzone struktury
Spintronika fotonika: analogie
 : analogie Paweł Wójcik, Maciej Wołoszyn, Bartłomiej Spisak W oparciu o wykład wygłoszony podczas konferencji 2nd World Congress of Smart Materials, Singapur, March 2-6, 2016 Wprowadzenie dla niespecjalistów
: analogie Paweł Wójcik, Maciej Wołoszyn, Bartłomiej Spisak W oparciu o wykład wygłoszony podczas konferencji 2nd World Congress of Smart Materials, Singapur, March 2-6, 2016 Wprowadzenie dla niespecjalistów
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 2, Mateusz Winkowski, Jan Szczepanek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 2, 06.10.2017 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Jan Szczepanek Radosław Łapkiewicz Równania Maxwella r-nie
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 2, 06.10.2017 wykład: pokazy: ćwiczenia: Czesław Radzewicz Mateusz Winkowski, Jan Szczepanek Radosław Łapkiewicz Równania Maxwella r-nie
Oddziaływanie atomu z kwantowym polem E-M: C.D.
 Oddziaływanie atomu z kwantowym polem E-M: C.D. 1 atom jakoźródło 1 fotonu. Emisja spontaniczna wg. złotej reguły Fermiego. Absorpcja i emisja kolektywna ˆ E( x,t)=i λ Powtórzenie d 3 ω k k 2ǫ(2π) 3 e
Oddziaływanie atomu z kwantowym polem E-M: C.D. 1 atom jakoźródło 1 fotonu. Emisja spontaniczna wg. złotej reguły Fermiego. Absorpcja i emisja kolektywna ˆ E( x,t)=i λ Powtórzenie d 3 ω k k 2ǫ(2π) 3 e
Metody optyczne w badaniach półprzewodników Przykładami różnymi zilustrowane. Piotr Perlin Instytut Wysokich Ciśnień PAN
 Metody optyczne w badaniach półprzewodników Przykładami różnymi zilustrowane Piotr Perlin Instytut Wysokich Ciśnień PAN Jak i czym scharakteryzować kryształ półprzewodnika Struktura dyfrakcja rentgenowska
Metody optyczne w badaniach półprzewodników Przykładami różnymi zilustrowane Piotr Perlin Instytut Wysokich Ciśnień PAN Jak i czym scharakteryzować kryształ półprzewodnika Struktura dyfrakcja rentgenowska
Stałe : h=6, Js h= 4, eVs 1eV= J nie zależy
 T_atom-All 1 Nazwisko i imię klasa Stałe : h=6,626 10 34 Js h= 4,14 10 15 evs 1eV=1.60217657 10-19 J Zaznacz zjawiska świadczące o falowej naturze światła a) zjawisko fotoelektryczne b) interferencja c)
T_atom-All 1 Nazwisko i imię klasa Stałe : h=6,626 10 34 Js h= 4,14 10 15 evs 1eV=1.60217657 10-19 J Zaznacz zjawiska świadczące o falowej naturze światła a) zjawisko fotoelektryczne b) interferencja c)
WYKŁAD 2 Podstawy spektroskopii wibracyjnej, model oscylatora harmonicznego i anharmonicznego. Częstość oscylacji a struktura molekuły Prof. dr hab.
 WYKŁAD 2 Podstawy spektroskopii wibracyjnej, model oscylatora harmonicznego i anharmonicznego. Częstość oscylacji a struktura molekuły Prof. dr hab. Halina Abramczyk POLITECHNIKA ŁÓDZKA Wydział Chemiczny
WYKŁAD 2 Podstawy spektroskopii wibracyjnej, model oscylatora harmonicznego i anharmonicznego. Częstość oscylacji a struktura molekuły Prof. dr hab. Halina Abramczyk POLITECHNIKA ŁÓDZKA Wydział Chemiczny
Podsumowanie W Spektroskopia dwufotonowa. 1. Spektroskopia nasyceniowa. selekcja prędkości. nasycenie. ω 0 ω Laser. ω 21 2ω.
 Podsumowanie W1 Lasery w spektroskopii atomowej/molekularnej a) spektroskopia klasyczna b) spektroskopia bezdopplerowska 1. Spektroskopia nasyceniowa nasycenie selekcja prędkości - wiązki pompująca & próbkująca
Podsumowanie W1 Lasery w spektroskopii atomowej/molekularnej a) spektroskopia klasyczna b) spektroskopia bezdopplerowska 1. Spektroskopia nasyceniowa nasycenie selekcja prędkości - wiązki pompująca & próbkująca
Spektroskopia charakterystycznych strat energii elektronów EELS (Electron Energy-Loss Spectroscopy)
 Spektroskopia charakterystycznych strat energii elektronów EELS (Electron Energy-Loss Spectroscopy) Oddziaływanie elektronów ze stałą, krystaliczną próbką wstecznie rozproszone elektrony elektrony pierwotne
Spektroskopia charakterystycznych strat energii elektronów EELS (Electron Energy-Loss Spectroscopy) Oddziaływanie elektronów ze stałą, krystaliczną próbką wstecznie rozproszone elektrony elektrony pierwotne
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki
 OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 006 Instytut Fizyki Uniwersytetu Szczecińskiego Równania (3.7), pomimo swojej prostoty, nie posiadają poza nielicznymi przypadkami ścisłych rozwiązań,
OPTYKA KWANTOWA Wykład dla 5. roku Fizyki c Adam Bechler 006 Instytut Fizyki Uniwersytetu Szczecińskiego Równania (3.7), pomimo swojej prostoty, nie posiadają poza nielicznymi przypadkami ścisłych rozwiązań,
Tak określił mechanikę kwantową laureat nagrody Nobla Ryszard Feynman ( ) mechanika kwantowa opisuje naturę w sposób prawdziwy, jako absurd.
 Tak określił mechanikę kwantową laureat nagrody Nobla Ryszard Feynman (1918-1988) mechanika kwantowa opisuje naturę w sposób prawdziwy, jako absurd. Równocześnie Feynman podkreślił, że obliczenia mechaniki
Tak określił mechanikę kwantową laureat nagrody Nobla Ryszard Feynman (1918-1988) mechanika kwantowa opisuje naturę w sposób prawdziwy, jako absurd. Równocześnie Feynman podkreślił, że obliczenia mechaniki
III Pracownia Półprzewodnikowa
 Pomiary czasowo-rozdzielcze nanostruktur azotkowych. Ćwiczenie będzie polegało na zmierzeniu czasowo-rozdzielonej fotoluminescencji przy użyciu kamery smugowej, a następnie na analizie otrzymanych danych.
Pomiary czasowo-rozdzielcze nanostruktur azotkowych. Ćwiczenie będzie polegało na zmierzeniu czasowo-rozdzielonej fotoluminescencji przy użyciu kamery smugowej, a następnie na analizie otrzymanych danych.
- wiązki pompująca & próbkująca oddziaływanie selektywne prędkościowo widma bezdopplerowskie. 0 k. z L 0 k. L 0 k
 Podsumowanie W1 Lasery w spektroskopii atomowej/molekularnej a) spektroskopia klasyczna b) spektroskopia bezdopplerowska 1. Spektroskopia nasyceniowa nasycenie selekcja prędkości - wiązki pompująca & próbkująca
Podsumowanie W1 Lasery w spektroskopii atomowej/molekularnej a) spektroskopia klasyczna b) spektroskopia bezdopplerowska 1. Spektroskopia nasyceniowa nasycenie selekcja prędkości - wiązki pompująca & próbkująca
Cel wykładu. Detekcja światła. Cel wykładu. Światło. Sebastian Maćkowski
 Cel wykładu Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje: czwartek
Cel wykładu Detekcja światła Sebastian Maćkowski Instytut Fizyki Uniwersytet Mikołaja Kopernika Adres poczty elektronicznej: mackowski@fizyka.umk.pl Biuro: 365, telefon: 611-3250 Konsultacje: czwartek
Podsumowanie W9. Wojciech Gawlik - Wstęp do Fizyki Atomowej, 2003/04. wykład 12 1
 Podsumowanie W9 Obserwacja przejść rezonansowych wymuszonych przez pole EM jest moŝliwa tylko, gdy istnieje róŝnica populacji. Tymczasem w zakresie fal radiowych poziomy są prawie jednakowo obsadzone.
Podsumowanie W9 Obserwacja przejść rezonansowych wymuszonych przez pole EM jest moŝliwa tylko, gdy istnieje róŝnica populacji. Tymczasem w zakresie fal radiowych poziomy są prawie jednakowo obsadzone.
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej. wykład 2, Radosław Chrapkiewicz, Filip Ozimek
 Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 2, 17.02.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Równania Maxwella r-nie falowe
Podstawy Fizyki IV Optyka z elementami fizyki współczesnej wykład 2, 17.02.2012 wykład: pokazy: ćwiczenia: Czesław Radzewicz Radosław Chrapkiewicz, Filip Ozimek Ernest Grodner Równania Maxwella r-nie falowe
III Pracownia Półprzewodnikowa
 Pomiary czasowo-rozdzielcze nanostruktur azotkowych. Ćwiczenie będzie polegało na zmierzeniu czasowo-rozdzielonej fotoluminescencji przy użyciu kamery smugowej, a następnie na analizie otrzymanych danych.
Pomiary czasowo-rozdzielcze nanostruktur azotkowych. Ćwiczenie będzie polegało na zmierzeniu czasowo-rozdzielonej fotoluminescencji przy użyciu kamery smugowej, a następnie na analizie otrzymanych danych.
Charakteryzacja właściwości elektronowych i optycznych struktur AlGaN GaN Dagmara Pundyk
 Charakteryzacja właściwości elektronowych i optycznych struktur AlGaN GaN Dagmara Pundyk Promotor: dr hab. inż. Bogusława Adamowicz, prof. Pol. Śl. Zadania pracy Pomiary transmisji i odbicia optycznego
Charakteryzacja właściwości elektronowych i optycznych struktur AlGaN GaN Dagmara Pundyk Promotor: dr hab. inż. Bogusława Adamowicz, prof. Pol. Śl. Zadania pracy Pomiary transmisji i odbicia optycznego
Atomy w zewnętrznym polu magnetycznym i elektrycznym
 Atomy w zewnętrznym polu magnetycznym i elektrycznym 1. Kwantowanie przestrzenne momentów magnetycznych i rezonans spinowy 2. Efekt Zeemana (normalny i anomalny) oraz zjawisko Paschena-Backa 3. Efekt Starka
Atomy w zewnętrznym polu magnetycznym i elektrycznym 1. Kwantowanie przestrzenne momentów magnetycznych i rezonans spinowy 2. Efekt Zeemana (normalny i anomalny) oraz zjawisko Paschena-Backa 3. Efekt Starka
V. KWANTOWE BRAMKI LOGICZNE Janusz Adamowski
 V. KWANTOWE BRAMKI LOGICZNE Janusz Adamowski 1 1 Wprowadzenie Wykład ten poświęcony jest dokładniejszemu omówieniu własności kwantowych bramek logicznych (kwantowych operacji logicznych). Podstawowymi
V. KWANTOWE BRAMKI LOGICZNE Janusz Adamowski 1 1 Wprowadzenie Wykład ten poświęcony jest dokładniejszemu omówieniu własności kwantowych bramek logicznych (kwantowych operacji logicznych). Podstawowymi
UMO-2011/01/B/ST7/06234
 Załącznik nr 7 do sprawozdania merytorycznego z realizacji projektu badawczego Szybka nieliniowość fotorefrakcyjna w światłowodach półprzewodnikowych do zastosowań w elementach optoelektroniki zintegrowanej
Załącznik nr 7 do sprawozdania merytorycznego z realizacji projektu badawczego Szybka nieliniowość fotorefrakcyjna w światłowodach półprzewodnikowych do zastosowań w elementach optoelektroniki zintegrowanej
WYKŁAD 8. Maria Krawczyk, Wydział Fizyki UW. Oddziaływania słabe
 Wszechświat cząstek elementarnych WYKŁAD 8 Maria Krawczyk, Wydział Fizyki UW Oddziaływania słabe Cztery podstawowe siłyprzypomnienie Oddziaływanie grawitacyjne Działa między wszystkimi cząstkami, jest
Wszechświat cząstek elementarnych WYKŁAD 8 Maria Krawczyk, Wydział Fizyki UW Oddziaływania słabe Cztery podstawowe siłyprzypomnienie Oddziaływanie grawitacyjne Działa między wszystkimi cząstkami, jest
ostawa. Fizyka powierzchni i nanostruktury 4
 Obrazy dyfrakcyjne elektronów Jak badać strukturę powierzchni? Własności: Dyfrakcja elektronowa cd. Dyfrakcja zachowuje symetrię. Duże odległości w obrazie dyfrakcyjnym oznaczają małe odległości na powierzchni.
Obrazy dyfrakcyjne elektronów Jak badać strukturę powierzchni? Własności: Dyfrakcja elektronowa cd. Dyfrakcja zachowuje symetrię. Duże odległości w obrazie dyfrakcyjnym oznaczają małe odległości na powierzchni.
Historia. Zasada Działania
 Komputer kwantowy układ fizyczny do opisu którego wymagana jest mechanika kwantowa, zaprojektowany tak, aby wynik ewolucji tego układu reprezentował rozwiązanie określonego problemu obliczeniowego. Historia
Komputer kwantowy układ fizyczny do opisu którego wymagana jest mechanika kwantowa, zaprojektowany tak, aby wynik ewolucji tego układu reprezentował rozwiązanie określonego problemu obliczeniowego. Historia
Propozycje tematów prac licencjackich dla studentów studiów indywidualnych z ZFCS na rok 2016/17
 Propozycje tematów prac licencjackich dla studentów studiów indywidualnych z ZFCS na rok 2016/17 Rentgenowskie badania interkalowanych wielowarstw grafenowych. Opiekun: dr hab. Grzegorz Kowalski, tel.
Propozycje tematów prac licencjackich dla studentów studiów indywidualnych z ZFCS na rok 2016/17 Rentgenowskie badania interkalowanych wielowarstw grafenowych. Opiekun: dr hab. Grzegorz Kowalski, tel.
Kwantowe stany splątane. Karol Życzkowski Instytut Fizyki, Uniwersytet Jagielloński 25 kwietnia 2017
 B l i ż e j N a u k i Kwantowe stany splątane Karol Życzkowski Instytut Fizyki, Uniwersytet Jagielloński 25 kwietnia 2017 Co to jest fizyka? Kopnij piłkę! Co to jest fizyka? Kopnij piłkę! Kup lody i poczekaj
B l i ż e j N a u k i Kwantowe stany splątane Karol Życzkowski Instytut Fizyki, Uniwersytet Jagielloński 25 kwietnia 2017 Co to jest fizyka? Kopnij piłkę! Co to jest fizyka? Kopnij piłkę! Kup lody i poczekaj
